BOJ 1005 ACM Craft

https://www.acmicpc.net/problem/1005

문제

서기 2012년! 드디어 2년간 수많은 국민들을 기다리게 한 게임 ACM Craft (Association of Construction Manager Craft)가 발매되었다.

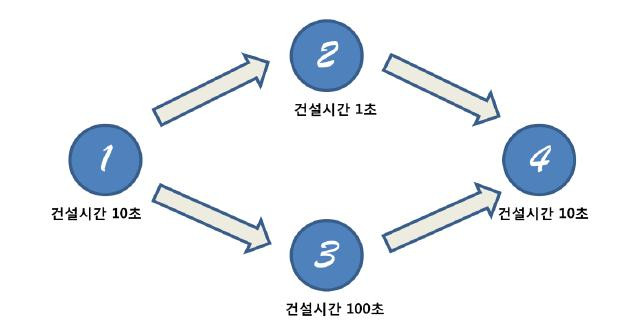
위의 예시를 보자.

이번 게임에서는 다음과 같이 건설 순서 규칙이 주어졌다. 1번 건물의 건설이 완료된다면 2번과 3번의 건설을 시작할수 있다. (동시에 진행이 가능하다) 그리고 4번 건물을 짓기 위해서는 2번과 3번 건물이 모두 건설 완료되어야지만 4번건물의 건설을 시작할수 있다.

따라서 4번건물의 건설을 완료하기 위해서는 우선 처음 1번 건물을 건설하는데 10초가 소요된다. 그리고 2번 건물과 3번 건물을 동시에 건설하기 시작하면 2번은 1초뒤에 건설이 완료되지만 아직 3번 건물이 완료되지 않았으므로 4번 건물을 건설할 수 없다. 3번 건물이 완성되고 나면 그때 4번 건물을 지을수 있으므로 4번 건물이 완성되기까지는 총 120초가 소요된다.

프로게이머 최백준은 애인과의 데이트 비용을 마련하기 위해 서강대학교배 ACM크래프트 대회에 참가했다! 최백준은 화려한 컨트롤 실력을 가지고 있기 때문에 모든 경기에서 특정 건물만 짓는다면 무조건 게임에서 이길 수 있다. 그러나 매 게임마다 특정건물을 짓기 위한 순서가 달라지므로 최백준은 좌절하고 있었다. 백준이를 위해 특정건물을 가장 빨리 지을 때까지 걸리는 최소시간을 알아내는 프로그램을 작성해주자.

---

입력

첫째 줄에는 테스트케이스의 개수 T가 주어진다. 각 테스트 케이스는 다음과 같이 주어진다. 첫째 줄에 건물의 개수 N과 건물간의 건설순서 규칙의 총 개수 K이 주어진다. (건물의 번호는 1번부터 N번까지 존재한다)

둘째 줄에는 각 건물당 건설에 걸리는 시간 $D_1, D_2, …, D_N$이 공백을 사이로 주어진다. 셋째 줄부터 K+2줄까지 건설순서 X Y가 주어진다. (이는 건물 X를 지은 다음에 건물 Y를 짓는 것이 가능하다는 의미이다)

마지막 줄에는 백준이가 승리하기 위해 건설해야 할 건물의 번호 W가 주어진다.

---

출력

건물 W를 건설완료 하는데 드는 최소 시간을 출력한다. 편의상 건물을 짓는 명령을 내리는 데는 시간이 소요되지 않는다고 가정한다.

건설순서는 모든 건물이 건설 가능하도록 주어진다.

---

제한

• 2 ≤ N ≤ 1000
• 1 ≤ K ≤ 100,000
• 1 ≤ X, Y, W ≤ N
• 0 ≤ $D_i$ ≤ 100,000, $D_i$는 정수

---

예제 입력 1

2
4 4
10 1 100 10
1 2
1 3
2 4
3 4
4
8 8
10 20 1 5 8 7 1 43
1 2
1 3
2 4
2 5
3 6
5 7
6 7
7 8
7

예제 출력 1

120
39

예제 입력 2

5
3 2
1 2 3
3 2
2 1
1
4 3
5 5 5 5
1 2
1 3
2 3
4
5 10
100000 99999 99997 99994 99990
4 5
3 5
3 4
2 5
2 4
2 3
1 5
1 4
1 3
1 2
4
4 3
1 1 1 1
1 2
3 2
1 4
4
7 8
0 0 0 0 0 0 0
1 2
1 3
2 4
3 4
4 5
4 6
5 7
6 7
7

예제 출력 2

6
5
399990
2
0

---

코드

특정 건물을 짓기 위해 드는 시간은 특정 건물을 지을 때 드는 시간 + 특정 건물을 짓기 위해 지어야 하는 건물 중 가장 오래 소요되는 시간이다.

그리고 반복된 시간 측정을 막기 위해 특정 건물을 지을 때 드는 시간을 계산했으면, 메모이제이션 해놓으면 된다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.StringTokenizer;

public class Main {

    static int[] timeRequired;
    static int[] totalTimeRequired;
    static List<Integer>[] conditions;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder answers = new StringBuilder();
        int T = Integer.parseInt(br.readLine());

        for (int i = 0; i < T; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int N = Integer.parseInt(st.nextToken());
            int K = Integer.parseInt(st.nextToken());
            timeRequired = new int[N + 1];
            totalTimeRequired = new int[N + 1];
            conditions = new List[N + 1];

            // 최소 0초로 지을 수 있는 건물이 있기 때문에, 검사하지 않음을 표시하기 위해 -1로 초기화
            Arrays.fill(totalTimeRequired, -1);

            st = new StringTokenizer(br.readLine());
            for (int j = 1; j <= N; j++) {
                timeRequired[j] = Integer.parseInt(st.nextToken());
                conditions[j] = new ArrayList<>();
            }

            for (int j = 0; j < K; j++) {
                st = new StringTokenizer(br.readLine());
                int condition = Integer.parseInt(st.nextToken());
                int target = Integer.parseInt(st.nextToken());
                conditions[target].add(condition);
            }

            int W = Integer.parseInt(br.readLine());

            answers.append(getTimeRequired(W)).append('\n');
        }

        System.out.println(answers);
    }

    static int getTimeRequired(int building) {
        if(totalTimeRequired[building] >= 0) {
            return totalTimeRequired[building];
        }

        int maxTimeRequired = 0;

        for (int check: conditions[building]) {
            maxTimeRequired = Integer.max(maxTimeRequired, getTimeRequired(check));
        }

        return totalTimeRequired[building] = timeRequired[building] + maxTimeRequired;
    }
}