BOJ 10473 인간 대포
https://www.acmicpc.net/problem/10473
문제
당신은 세계적인 인간대포 서커스 공연자이다. 즉, 당신은 거대한 가짜 대포 안으로 기어올라가 먼 거리를 발사되며 사람들에게 기쁨을 주는 사람인 것이다. 오늘, 당신은 혼자가 아니다. 당신은 국제 인간대포 회의 겸 전시장에 와 있으며 이 곳에서는 수백명의 인간대포 전문가들이 서로의 경험을 공유하고 기술을 연마한다. 보통 당신의 서커스에서 당신은 한 대포만을 가지고 공연하는데 반해 이곳에서는 사용할 수 있는 수많은 대포가 있다.
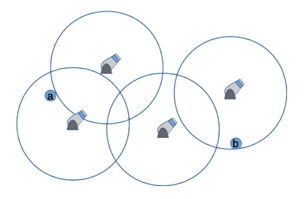
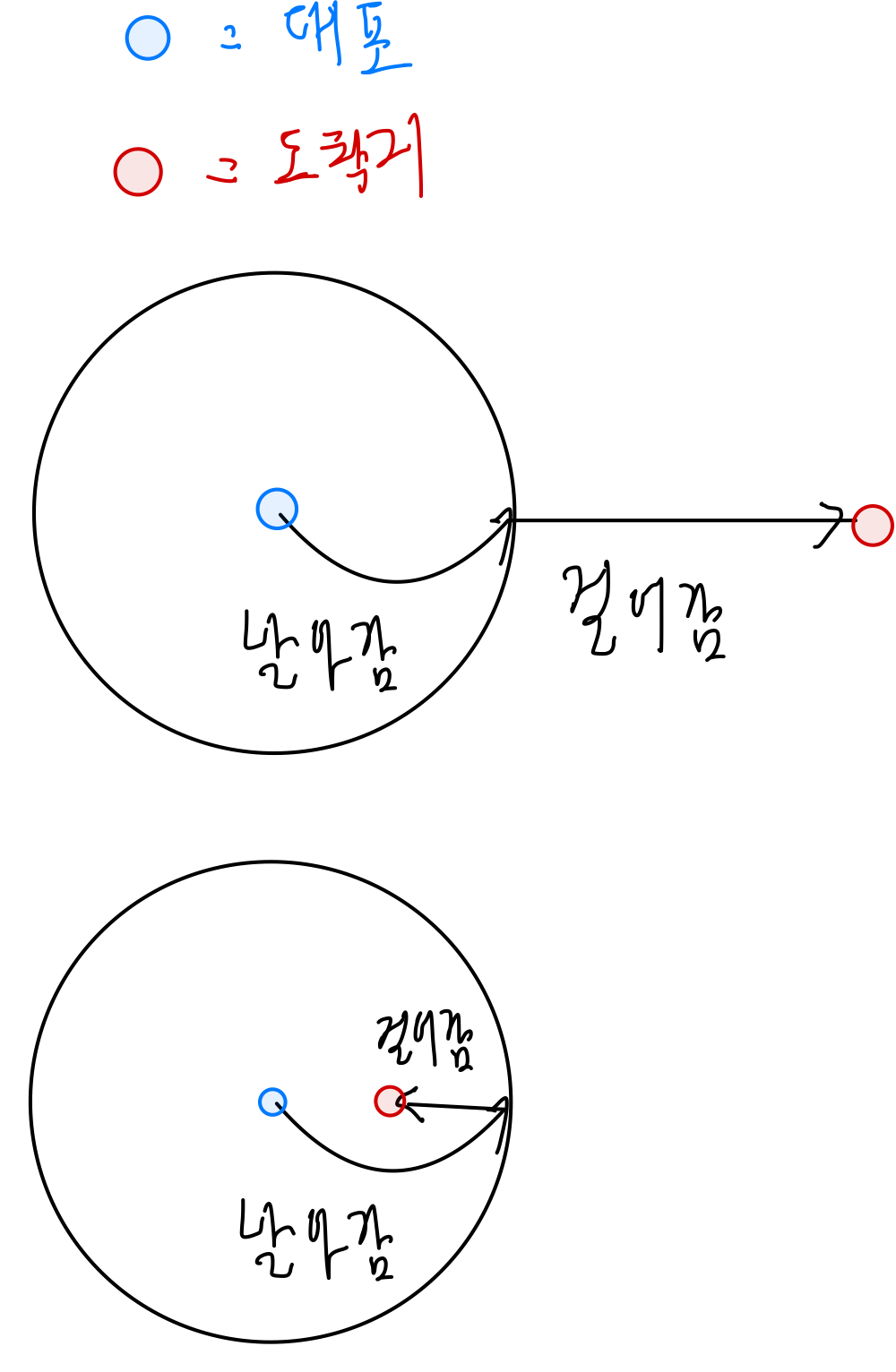
여러 대포를 사용하면 회의장을 좀 더 편리하게 돌아다닐 수 있다. 만약 당신이 a장소에서 b장소까지 이동하려 한다면 a 부터 b까지 직선으로 걸어갈 수도 있고, 주변의 대포에 탑승해서 어딘가 다른 곳으로 발사되어 이동할 수도 있다. 발사되고 나면 내린 위치에서 도착점을 향해서 걸어갈 수도 있고, 다시 한 번 또 다른 대포를 이용하여 목적지에 더 빠르게 도착할 수도 있다. 그림 E.1처럼 배치된 지도에서 당신은 a에서 b로 이동하기 위하여 그림 E.2와 같은 경로로 걷거나 대포를 이용하여 움직일 수 있다. 화살표는 당신이 대포에서 발사되어 떨어진 점을 의미하며 직선은 당신이 달린 경로를 나타낸다.
당신은 5m/s의 속도로 달린다. 모든 대포는 당신을 당신이 원하는 임의의 방향으로 50m 날려줄 수 있다. 대포에 올라타고 발사되고 착륙하기까지는 정확히 2초가 걸린다. 대포는 장애물이 아니기 때문에 당신이 뛰는 도중에 대포가 있다면 점프해서 넘어가 마치 직선과 같이 움직일 수 있다. 당신의 현재 위치와 목적지의 위치, 그리고 대포들의 위치가 주어질 때 당신은 목적지에 가장 빨리가기 위한 경로를 알고 싶다.
입력
입력은 한 개의 길찾기 문제를 표현한다. 첫 줄에는 두 개의 실수가 입력되며 각각은 당신이 현재 위치한 X, Y좌표이다. 두 번째 줄에는 목적지의 X, Y좌표가 실수로 입력된다. 이어지는 줄에는 대포의 숫자 정수 n이 주어진다. 남은 n줄에는 한 줄에 대포 하나의 위치 정보가 주어지며, 이는 실수로 주어지는 X, Y 좌표이다. 모든 좌표는 미터로 측정되었으며 n의 값은 0 이상 100 이하이다. 입력으로 주어지는 모든 X, Y좌표는 0 이상 500 이하의 실수이고, 소수점 아래로 최대 두 자리까지만 주어진다.
출력
한 줄에 걸쳐 목적지에 다다르기 위해 가장 빠른 시간을 출력하라. 실제 답과 0.001초 미만의 차이는 정답으로 인정한다.
예제 입력 1
25.0 100.0 190.0 57.5 4 125.0 67.5 75.0 125.0 45.0 72.5 185.0 102.5
예제 출력 1
19.984901
코드
출발지에서 도착지까지 도달하는데 걸리는 가장 빠른 시간을 계산해야 하는 문제이기 때문에 다익스트라를 사용하는 문제라고 생각했다.
다만, 일반적인 문제와 다르게 출발지, 도착지 혹은 대포의 위치가 실수 형태라는 것이었다.
BOJ 4485 녹색 옷 입은 애가 젤다지?에서 좌표가 나왔을 때는 이차원 배열을 이용해 상하좌우로 방문하며 풀었었다.
이번 문제도 “모든 X, Y좌표는 0 이상 500 이하의 실수이고, 소수점 아래로 최대 두 자리까지만 주어진다.” 고 나왔기 때문에 ‘각 좌표에 100을 곱해 정수로 만든 다음 이차원 배열로 풀어야 하는 건가?’ 라고 생각했지만, 이차원 배열로는 대포를 기준으로 원을 표현하기는 어려울 것 같았기 때문에 다른 방향으로 생각해봤다.
문제에서는 이동하는 방법이 걸어가는 것, 대포를 타고 이동하는 것으로 두가지가 있다고 나왔다.
이 말은 출발지에서는 대포가 없기 때문에 출발지에서 도착지로 곧장 가는 최소 시간은 직선으로 갔을 때 구할 수 있고, 다른 엄한 좌표는 생각하지 않아도 된다는 의미이다.
이것은 각 대포의 위치에서 다른 대포나 도착지로 가는 최소 시간도 위와 비슷하다는 것을 알 수 있다. 대포에서 다른 대포의 위치나 도착지로 가는 방법은 아래와 같다.
- 걸어서 간다.
- 대포를 타고 나머지 거리는 걸어서 간다.
1) 도착지가 대포에서 50m보다 멀리 있을 때
2) 도착지가 대포에서 50m 안에 있을 때
즉, 우리는 출발지, 도착지, 대포의 위치를 제외한 나머지 좌표는 생각할 필요가 없다는 뜻이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main {
static class Node implements Comparable<Node> {
int idx;
double time;
public Node(int idx, double time) {
this.idx = idx;
this.time = time;
}
@Override
public int compareTo(Node o) {
return time > o.time ? 1 : -1;
}
}
/**
* 입력받는 시작점, 도착점 및 대포의 위치를 저장하기 위한 클래스
* java.awt.Point 클래스는 각각의 X, Y를 int형으로 저장하기 때문에 사용할 수 없다.
*/
static class Place {
double r, c;
public Place(double r, double c) {
this.r = r;
this.c = c;
}
}
static int N;
static double[] minTimes; // 출발지에서 i번째 장소까지 가는데 걸리는 최소 시간을 저장하는 배열
static double[][] travelTimes; // a번째 장소에서 b번째 장소까지 가는데 걸리는 시간을 저장하는 배열
static Place[] places; // 입력받는 시작점, 도착점 및 대포의 위치를 저장하는 배열
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
// 시작점
Place start = new Place(Double.parseDouble(st.nextToken()), Double.parseDouble(st.nextToken()));
st = new StringTokenizer(br.readLine());
// 도착점
Place end = new Place(Double.parseDouble(st.nextToken()), Double.parseDouble(st.nextToken()));
N = Integer.parseInt(br.readLine());
places = new Place[N + 2]; // 시작점과 도착점을 포함하여 배열에 저장하기 위해 N+2 크기로 초기화
places[0] = start;
places[N + 1] = end;
// 나머지 대포의 위치를 입력받는다
for (int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine());
places[i] = new Place(Double.parseDouble(st.nextToken()), Double.parseDouble(st.nextToken()));
}
minTimes = new double[N + 2];
for (int i = 1; i < N + 2; i++) minTimes[i] = 5000.0;
// 장소 a에서 b로 곧장 가는 최소 시간을 미리 계산
travelTimes = new double[N + 2][N + 2];
// 출발지에서 특정 장소로 가는 시간은 걸어가는 시간 밖에 없음
for (int i = 1; i < N + 2; i++) {
travelTimes[0][i] = getDistance(places[0], places[i]) / 5;
}
/**
* 출발지와 목적지를 제외한 나머지 장소는 대포이므로
* 장소 a에서 b로 곧장 가는 시간은 걸어가는 시간과
* 대포를 타고 남은 거리를 걸어가는 시간 중 짧은 시간이다.
*/
for (int i = 1; i <= N; i++) {
for (int j = 1; j < N + 2; j++) {
double distance = getDistance(places[i], places[j]);
// 대포로 가는 시간은 목적지가 50m 밖이든 안이든 대포를 타고 간 장소에서 목적지까지 남은 거리를 걷는 시간 + 대포를 타는 시간 2이다.
travelTimes[i][j] = Double.min(distance / 5, Math.abs(distance - 50) / 5 + 2);
}
}
dijkstra();
System.out.println(minTimes[N + 1]);
}
static void dijkstra() {
PriorityQueue<Node> queue = new PriorityQueue<>();
queue.offer(new Node(0, 0));
while (!queue.isEmpty()) {
Node check = queue.poll();
for (int i = 1; i < N + 2; i++) {
if(minTimes[i] > check.time + travelTimes[check.idx][i]) {
minTimes[i] = check.time + travelTimes[check.idx][i];
queue.offer(new Node(i, minTimes[i]));
}
}
}
}
// 두 장소 사이의 거리를 계산하는 메소드
static double getDistance(Place a, Place b) {
return Math.sqrt(Math.pow(a.r - b.r, 2) + Math.pow(a.c - b.c, 2));
}
}