BOJ 13334 철로

https://www.acmicpc.net/problem/13334

문제

집과 사무실을 통근하는 n명의 사람들이 있다. 각 사람의 집과 사무실은 수평선 상에 있는 서로 다른 점에 위치하고 있다. 임의의 두 사람 A, B에 대하여, A의 집 혹은 사무실의 위치가 B의 집 혹은 사무실의 위치와 같을 수 있다. 통근을 하는 사람들의 편의를 위하여 일직선 상의 어떤 두 점을 잇는 철로를 건설하여, 기차를 운행하려고 한다. 제한된 예산 때문에, 철로의 길이는 d로 정해져 있다. 집과 사무실의 위치 모두 철로 선분에 포함되는 사람들의 수가 최대가 되도록, 철로 선분을 정하고자 한다.

양의 정수 d와 n 개의 정수쌍, $(h_i, o_i), 1 ≤ i ≤ n$,이 주어져 있다. 여기서 $h_i$와 $o_i$는 사람 $i$의 집과 사무실의 위치이다. 길이 d의 모든 선분 L에 대하여, 집과 사무실의 위치가 모두 L에 포함되는 사람들의 최대 수를 구하는 프로그램을 작성하시오.

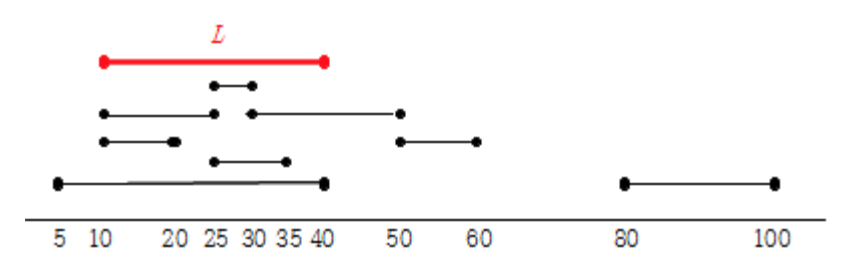
그림 1 에 있는 예를 고려해보자. 여기서 $n = 8$, $(h_1, o_1) = (5, 40)$, $(h_2, o_2) = (35, 25)$, $(h_3, o_3) = (10, 20)$, $(h_4, o_4) = (10, 25)$, $(h_5, o_5) = (30, 50)$, $(h_6, o_6) = (50, 60)$, $(h_7, o_7) = (30, 25)$, $(h_8, o_8) = (80, 100)$이고, d = 30이다. 이 예에서, 위치 10 과 40 사이의 빨간색 선분 L이, 가장 많은 사람들에 대하여 집과 사무실 위치 모두 포함되는 선분 중 하나이다. 따라서 답은 4 이다.

---

입력

입력은 표준입력을 사용한다. 첫 번째 줄에 사람 수를 나타내는 양의 정수 n (1 ≤ n ≤ 100,000)이 주어진다. 다음 n개의 각 줄에 정수 쌍 $(h_i, o_i)$가 주어진다. 여기서 $h_i$와 $o_i$는 −100,000,000이상, 100,000,000이하의 서로 다른 정수이다. 마지막 줄에, 철로의 길이를 나타내는 정수 d (1 ≤ d ≤ 200,000,000)가 주어진다.

---

출력

출력은 표준출력을 사용한다. 길이 d의 임의의 선분에 대하여, 집과 사무실 위치가 모두 그 선분에 포함되는 사람들의 최대 수를 한 줄에 출력한다.

---

예제 입력 1

8
5 40
35 25
10 20
10 25
30 50
50 60
30 25
80 100
30

예제 출력 1

4

예제 입력 2

4
20 80
70 30
35 65
40 60
10

예제 출력 2

0

… 이하 예제 생략

---

코드

각 선분이 특정 범위 안에 있는지 전부 확인해야 하는 문제이기 때문에 DP나 그리디를 사용해서 해결하는 문제가 아니라고 생각했다.

첫 시도는 별 생각없이 경로의 출발점을 기준으로 오름차순 정렬하고, 각 경로의 출발점부터 d 이내에 있는 경로의 수를 카운트했지만, 시간 초과가 발생했다.

중복되는 검사를 여러 번 하는 것이 문제라고 생각했고, 우선순위 큐를 사용하는 알고리즘을 생각해서 문제를 해결했다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.StringTokenizer;

public class Main {

    static class Way {
        int start;
        int end;

        public Way(int start, int end) {
            this.start = start;
            this.end = end;
        }
    }

    static int n;
    static int d;
    static PriorityQueue<Way> ways = new PriorityQueue<>(Comparator.comparingInt(way -> way.end));

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.parseInt(br.readLine());
        for (int i = 0; i < n; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            int start = Integer.parseInt(st.nextToken());
            int end = Integer.parseInt(st.nextToken());

            Way newWay;
            // 경로의 양 끝 점 중 작은 쪽이 Way의 start, 큰 쪽이 Way의 end가 되게 함
            if(start < end) {
                newWay = new Way(start, end);
            } else {
                newWay = new Way(end, start);
            }

            ways.offer(newWay);
        }

        d = Integer.parseInt(br.readLine());

        int answer = calculateMaxWays();

        System.out.println(answer);
    }

    static int calculateMaxWays() {
        // 선분 L에 포함되어 있는 경로들을 보관하기 위한 우선순위 큐
        PriorityQueue<Way> included = new PriorityQueue<>(Comparator.comparingInt(way -> way.start));
        int maxWays = Integer.MIN_VALUE;

        // 입력받은 경로들을 도착 위치가 작은 순으로 검사한다.
        while (!ways.isEmpty()) {
            int endBoundary = ways.peek().end; // 선분 L의 끝
            int startBoundary = endBoundary - d; // 선분 L의 시작

            // 도착 위치가 선분 L 범위 내에 있는 경로들을 included 우선순위 큐에 추가
            while (!ways.isEmpty() && ways.peek().end == endBoundary) {
                included.offer(ways.poll());
            }

            // included 우선순위 큐에 있는 경로들 중 출발 위치가 선분 L 범위 내에 있지 않은 경로를 제거
            while (!included.isEmpty() && included.peek().start < startBoundary) {
                included.poll();
            }

            // included 우선순위 큐에 있는 경로의 수 중 최대값 계산
            maxWays = Integer.max(maxWays, included.size());
        }

        return maxWays;
    }
}