BOJ 14719 빗물

https://www.acmicpc.net/problem/14719

문제

2차원 세계에 블록이 쌓여있다. 비가 오면 블록 사이에 빗물이 고인다.

비는 충분히 많이 온다. 고이는 빗물의 총량은 얼마일까?

---

입력

첫 번째 줄에는 2차원 세계의 세로 길이 H과 2차원 세계의 가로 길이 W가 주어진다. (1 ≤ H, W ≤ 500)

두 번째 줄에는 블록이 쌓인 높이를 의미하는 0이상 H이하의 정수가 2차원 세계의 맨 왼쪽 위치부터 차례대로 W개 주어진다.

따라서 블록 내부의 빈 공간이 생길 수 없다. 또 2차원 세계의 바닥은 항상 막혀있다고 가정하여도 좋다.

---

출력

2차원 세계에서는 한 칸의 용량은 1이다. 고이는 빗물의 총량을 출력하여라.

빗물이 전혀 고이지 않을 경우 0을 출력하여라.

---

예제 입력 1

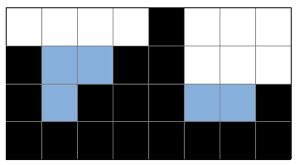
4 4
3 0 1 4

예제 출력 1

5

예제 입력 2

4 8
3 1 2 3 4 1 1 2

예제 출력 2

5

… 이하 예제 생략

---

코드

2차원 세계에서 i번째 블록에 고이는 빗물의 양은 i번째 블록의 높이, i번째 블록에서 봤을 때 왼쪽과 오른쪽에 있는 가장 높은 블록의 높이에 의해 결정된다.

예제 1번을 예로 들어보자.

두 번째 블록의 높이는 0이다.

그리고 두 번째 블록에서 봤을 때 왼쪽에서 가장 높은 블록의 높이는 3이고, 오른쪽에서 가장 높은 블록의 높이는 4이다.

이때, 두 번째 블록에 고이는 빗물의 양은 3(왼쪽에서 가장 높은 블록의 높이) - 0(두 번째 블록의 높이) = 3이다.

즉, i번째 블록에서 봤을 때 왼쪽에서 가장 높은 블록의 높이를 lHighest[i], 오른쪽에서 가장 높은 블록의 높이를 rHighest[i] 그리고 i번째 블록의 높이를 block[i]라고 하면

i번째 블록에서 고이는 빗물의 양 = min(lHighest[i], rHighest[i]) - block[i]

라고 볼 수 있다.

물론 위의 결과가 0보다 작거나 같은 수라면, 해당 칸에서는 물이 고이지 않는다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int H = Integer.parseInt(st.nextToken());
        int W = Integer.parseInt(st.nextToken());
        int[] block = new int[W];
        
        // lHighest, rHighest 는 각각 특정 위치에서 왼쪽과 오른쪽에 존재하는 가장 높은 블록의 높이를 저장하는 배열
        int[] lHighest = new int[W];
        int[] rHighest = new int[W];

        st = new StringTokenizer(br.readLine());

        // 2차원 세계의 블록의 높이를 입력받으며 특정 위치에서 왼쪽에 존재하는 가장 높은 블록의 높이를 저장
        block[0] = Integer.parseInt(st.nextToken());
        lHighest[0] = block[0];
        for (int i = 1; i < W; i++) {
            block[i] = Integer.parseInt(st.nextToken());
            lHighest[i] = Integer.max(block[i], lHighest[i - 1]);
        }

        // 특정 위치에서 오른쪽에 존재하는 가장 높은 블록의 높이를 저장
        rHighest[W - 1] = block[W - 1];
        for (int i = W - 2; i >= 0; i--) {
            rHighest[i] = Integer.max(block[i], rHighest[i + 1]);
        }

        
        int answer = 0;
        for (int i = 1; i < W; i++) {
            int maxHeight = Integer.min(lHighest[i], rHighest[i]);
            if(block[i] < maxHeight) {
                answer += maxHeight - block[i];
            }
        }

        System.out.println(answer);
    }
}