BOJ 16946 벽 부수고 이동하기 4

https://www.acmicpc.net/problem/16946

문제

N×M의 행렬로 표현되는 맵이 있다. 맵에서 0은 이동할 수 있는 곳을 나타내고, 1은 이동할 수 없는 벽이 있는 곳을 나타낸다. 한 칸에서 다른 칸으로 이동하려면, 두 칸이 인접해야 한다. 두 칸이 변을 공유할 때, 인접하다고 한다.

각각의 벽에 대해서 다음을 구해보려고 한다.

• 벽을 부수고 이동할 수 있는 곳으로 변경한다.
• 그 위치에서 이동할 수 있는 칸의 개수를 세어본다.

한 칸에서 이동할 수 있는 칸은 상하좌우로 인접한 칸이다.

---

입력

첫째 줄에 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 1,000)이 주어진다. 다음 N개의 줄에 M개의 숫자로 맵이 주어진다.

---

출력

맵의 형태로 정답을 출력한다. 원래 빈 칸인 곳은 0을 출력하고, 벽인 곳은 이동할 수 있는 칸의 개수를 10으로 나눈 나머지를 출력한다.

---

예제 입력 1

3 3
101
010
101

예제 출력 1

303
050
303

예제 입력 2

4 5
11001
00111
01010
10101

예제 출력 2

46003
00732
06040
50403

---

코드

이전에 풀었던 BOJ 2206 벽 부수고 이동하기 문제를 변형한 문제인 것 같다.

처음 문제를 봤을 때는 당연히 BFS가 떠올랐다.

하지만, 조금 더 효율적인 방법이 있을 것 같아서 생각해봤다.

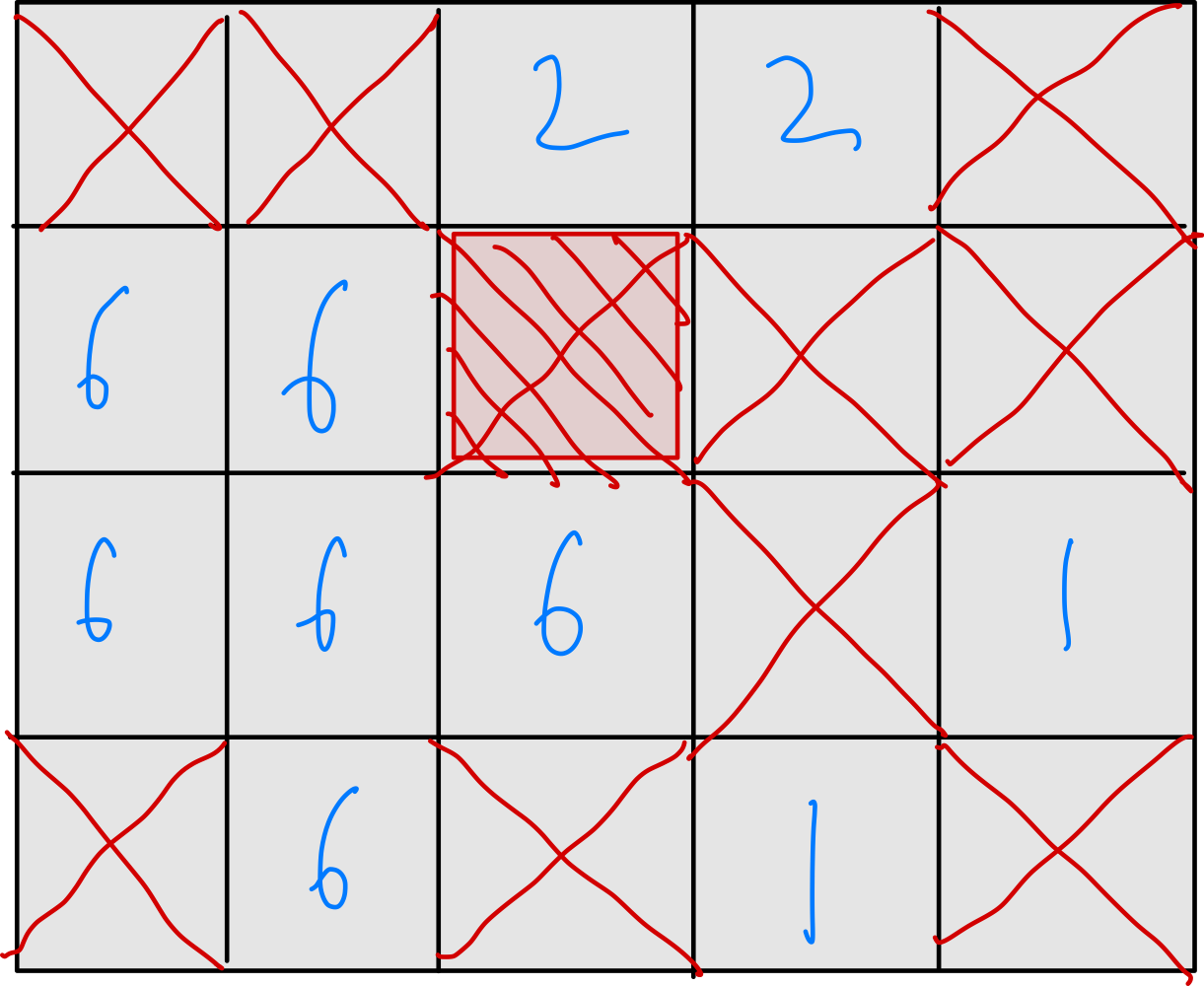
아래와 같이 맨 처음 맵의 상태를 입력받으면, 벽으로 나눠진 각 구역의 크기를 구할 수 있다. (X 표시는 벽)

위 상태에서 정답을 구하려면 각 벽을 없앴을 때, 각 벽에서 상, 하, 좌, 우 방향에 있는 구역의 크기를 더하면 해당 벽을 부쉈을 때 이동할 수 있는 칸의 개수를 쉽게 구할 수 있다.

다만, 주의해야 할 점은 상, 하, 좌, 우 방향에 있는 구역이 모두 다른 구역이라는 보장은 없다는 것이다.

예를 들어, 아래 그림에서 빨간색으로 채운 벽을 봤을 때, 해당 벽에서 왼쪽과 아래쪽에 있는 구역은 동일한 구역이다.

즉, 상, 하, 좌, 우 방향에 있는 구역 중 같은 구역이 아닌 구역의 크기들과 벽을 부순 곳 1을 더하면, 해당 벽에서 이동할 수 있는 칸의 개수를 구할 수 있다.

이를 위해, union-find 방식으로 각 구역에 있는 칸들의 부모를 하나로 지정하고, 같은 부모가 아닐 경우 다른 구역으로 판단하는 방식으로 풀었다.

import java.awt.*;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;

public class Main {

    static final int[] DIR_ROW = {1, -1, 0, 0};
    static final int[] DIR_COL = {0, 0, 1, -1};

    static int N;
    static int M;
    static boolean[][] map;
    static int[][] linked;
    static Point[][] parents;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());
        map = new boolean[N][M];
        linked = new int[N][M];
        parents = new Point[N][M];
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < M; j++) {
                int input = br.read();
                if(input == '1') {
                    map[i][j] = true;
                }
                parents[i][j] = new Point(i, j);
            }
            br.readLine();
        }

        for (int i = 0; i < N; i++) {
            for (int j = 0; j < M; j++) {
                if(!map[i][j] && parents[i][j].x == i && parents[i][j].y == j) {
                    linked[i][j] = search(i, j);
                }
            }
        }

        StringBuilder answer = new StringBuilder();
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < M; j++) {
                if(map[i][j]) {
                    answer.append(movable(i, j) % 10);
                } else {
                    answer.append(0);
                }
            }
            answer.append('\n');
        }

        System.out.println(answer);
    }

    static void union(int r1, int c1, int r2, int c2) {
        Point parents1 = find(r1, c1);
        Point parents2 = find(r2, c2);

        if(parents1.x < parents2.x || parents1.x == parents2.x && parents1.y < parents2.y) {
            parents[parents2.x][parents2.y] = parents1;
            return;
        }

        parents[parents1.x][parents1.y] = parents2;
    }

    static Point find(int r, int c) {
        Point p = parents[r][c];
        if(p.x == r && p.y == c) {
            return p;
        }

        return parents[r][c] = find(p.x, p.y);
    }

    static int search(int r, int c) {
        int link = 1; // 해당 구역의 칸을 카운트하기 위한 변수
        for (int i = 0; i < DIR_ROW.length; i++) {
            int newR = r + DIR_ROW[i];
            int newC = c + DIR_COL[i];
            // 상하좌우가 맵 안에 있고 해당 칸이 벽이 아니라면 탐색 진행
            if(newR >= 0 && newR < N && newC >= 0 && newC < M && !map[newR][newC]) {
                // 상하좌우에 있는 칸이 검사 중인 칸의 부모와 같지 않으면 union 하고 탐색 진행
                if(!find(r, c).equals(find(newR, newC))) {
                    union(r, c, newR, newC);
                    link += search(newR, newC);
                }
            }
        }
        return link;
    }

    static int movable(int r, int c) {
        int count = 1; // 벽을 부순 곳도 카운트해야 하기 때문에 1부터 시작
        List<Point> visited = new ArrayList<>();
        for (int i = 0; i < DIR_ROW.length; i++) {
            int newR = r + DIR_ROW[i];
            int newC = c + DIR_COL[i];
            if(newR >= 0 && newR < N && newC >= 0 && newC < M && !map[newR][newC]) {
                Point parent = find(newR, newC);
                if(!visited.contains(parent)) {
                    visited.add(parent);
                    count += linked[parent.x][parent.y];
                }
            }
        }

        return count;
    }
}