BOJ 1725 히스토그램

https://www.acmicpc.net/problem/1725

문제

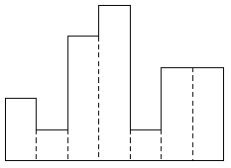
히스토그램에 대해서 알고 있는가? 히스토그램은 아래와 같은 막대그래프를 말한다.

각 칸의 간격은 일정하고, 높이는 어떤 정수로 주어진다. 위 그림의 경우 높이가 각각 2 1 4 5 1 3 3이다.

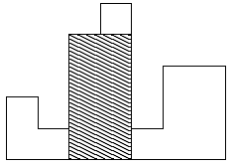
이러한 히스토그램의 내부에 가장 넓이가 큰 직사각형을 그리려고 한다. 아래 그림의 빗금 친 부분이 그 예이다. 이 직사각형의 밑변은 항상 히스토그램의 아랫변에 평행하게 그려져야 한다.

주어진 히스토그램에 대해, 가장 큰 직사각형의 넓이를 구하는 프로그램을 작성하시오.

---

입력

첫 행에는 N (1 ≤ N ≤ 100,000) 이 주어진다. N은 히스토그램의 가로 칸의 수이다. 다음 N 행에 걸쳐 각 칸의 높이가 왼쪽에서부터 차례대로 주어진다. 각 칸의 높이는 1,000,000,000보다 작거나 같은 자연수 또는 0이다.

---

출력

첫째 줄에 가장 큰 직사각형의 넓이를 출력한다. 이 값은 20억을 넘지 않는다.

---

예제 입력 1

7
2
1
4
5
1
3
3

예제 출력 1

8

---

코드

divide and conquer 방식으로 해결했다.

다음에는 스택을 이용해서 해결해보도록 하자.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
    static int[] inputs;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());
        inputs = new int[N];
        for (int i = 0; i < N; i++)
            inputs[i] = Integer.parseInt(br.readLine());

        System.out.println(calMaxArea(0, N - 1));
    }

    static int calMaxArea(int left, int right) {
        if(left == right) return inputs[left];

        int mid = (right + left) / 2;

        // 주어진 범위를 절반으로 나누어 왼쪽 구역의 최대 크기, 오른쪽 구역의 최대 크기, 중앙에서의 최대 크기를 비교 후 최대값 리턴
        return max(
                calMaxArea(left, mid),
                calMaxArea(mid + 1, right),
                checkMid(mid, left, right)
        );
    }

    static int checkMid(int mid, int left, int right) {
        int result = inputs[mid], lowest = inputs[mid], l = mid - 1, r = mid + 1;

        // 더 높은 막대 그래프가 있는 곳을 우선 탐색하며 해당 구역의 최대 크기를 계산함
        while (l >= left && r <= right) {
            int checkHeight = inputs[l] > inputs[r] ? inputs[l--] : inputs[r++];
            if(lowest > checkHeight) lowest = checkHeight;
            result = Integer.max(result, (r - l - 1) * lowest);
        }

        // 왼쪽이나 오른쪽 끝까지 탐색한 이후 나머지 구역을 탐색함
        for (; l >= left; l--) {
            if(lowest > inputs[l]) lowest = inputs[l];
            result = Integer.max(result, (r - l) * lowest);
        }
        for (; r <= right; r++) {
            if(lowest > inputs[r]) lowest = inputs[r];
            result = Integer.max(result, (r - l) * lowest);
        }

        return result;
    }

    static int max(int... inputs) {
        int max = Integer.MIN_VALUE;
        for (int input: inputs)
            if(max < input) max = input;

        return max;
    }
}