BOJ 20055 컨베이어 벨트 위의 로봇

https://www.acmicpc.net/problem/20055

문제

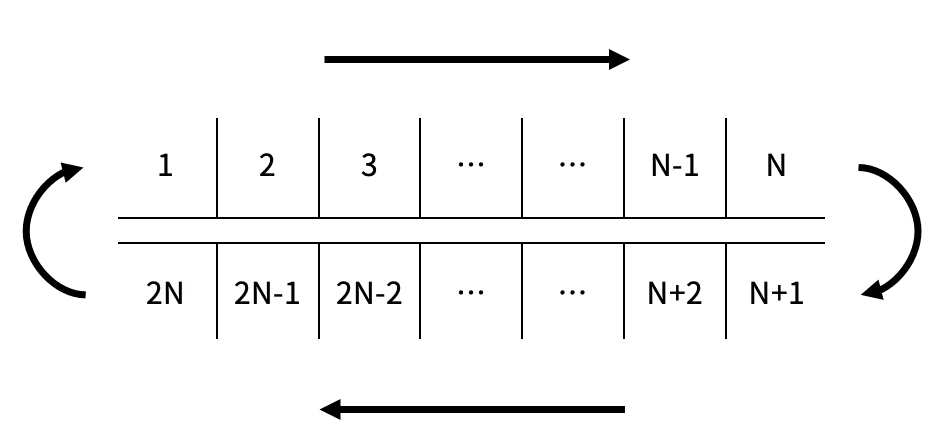
길이가 N인 컨베이어 벨트가 있고, 길이가 2N인 벨트가 이 컨베이어 벨트를 위아래로 감싸며 돌고 있다. 벨트는 길이 1 간격으로 2N개의 칸으로 나뉘어져 있으며, 각 칸에는 아래 그림과 같이 1부터 2N까지의 번호가 매겨져 있다.

벨트가 한 칸 회전하면 1번부터 2N-1번까지의 칸은 다음 번호의 칸이 있는 위치로 이동하고, 2N번 칸은 1번 칸의 위치로 이동한다. i번 칸의 내구도는 $A_i$이다. 위의 그림에서 1번 칸이 있는 위치를 “올리는 위치”, N번 칸이 있는 위치를 “내리는 위치“라고 한다.

컨베이어 벨트에 박스 모양 로봇을 하나씩 올리려고 한다. 로봇은 올리는 위치에만 올릴 수 있다. 언제든지 로봇이 내리는 위치에 도달하면 그 즉시 내린다. 로봇은 컨베이어 벨트 위에서 스스로 이동할 수 있다. 로봇을 올리는 위치에 올리거나 로봇이 어떤 칸으로 이동하면 그 칸의 내구도는 즉시 1만큼 감소한다.

컨베이어 벨트를 이용해 로봇들을 건너편으로 옮기려고 한다. 로봇을 옮기는 과정에서는 아래와 같은 일이 순서대로 일어난다.

1. 벨트가 각 칸 위에 있는 로봇과 함께 한 칸 회전한다.
2. 가장 먼저 벨트에 올라간 로봇부터, 벨트가 회전하는 방향으로 한 칸 이동할 수 있다면 이동한다. 만약 이동할 수 없다면 가만히 있는다.

   1. 로봇이 이동하기 위해서는 이동하려는 칸에 로봇이 없으며, 그 칸의 내구도가 1 이상 남아 있어야 한다.

3. 올리는 위치에 있는 칸의 내구도가 0이 아니면 올리는 위치에 로봇을 올린다.
4. 내구도가 0인 칸의 개수가 K개 이상이라면 과정을 종료한다. 그렇지 않다면 1번으로 돌아간다.

종료되었을 때 몇 번째 단계가 진행 중이었는지 구해보자. 가장 처음 수행되는 단계는 1번째 단계이다.

---

입력

첫째 줄에 N, K가 주어진다. 둘째 줄에는 $A_1, A_2, …, A_{2N}$이 주어진다.

---

출력

몇 번째 단계가 진행 중일때 종료되었는지 출력한다.

---

제한

• 2 ≤ N ≤ 100
• 1 ≤ K ≤ 2N
• 1 ≤ $A_i$ ≤ 1,000

---

예제 입력 1

3 2
1 2 1 2 1 2

예제 출력 1

2

예제 입력 2

3 6
10 10 10 10 10 10

예제 출력 2

31

… 이하 예제 생략

---

코드

지문이 조금 이해하기 힘들 수도 있지만, 단순 구현 문제였다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {

    static int zeroDurability = 0;
    static int upIdx = 0;
    static int downIdx;
    static int N;
    static int K;
    static int[] A;
    static boolean[] robots;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        K = Integer.parseInt(st.nextToken());
        downIdx = N - 1;
        A = new int[N * 2];
        robots = new boolean[N * 2];
        st = new StringTokenizer(br.readLine());
        for (int i = 0; i < N * 2; i++) {
            A[i] = Integer.parseInt(st.nextToken());
        }

        int answer = execute();
        System.out.println(answer);
    }

    static int execute() {
        int time = 0;

        do {
            stepOne();
            stepTwo();
            stepThree();
            time++;
        } while (zeroDurability < K);

        return time;
    }

    static void stepOne() {
        upIdx = rotate(upIdx);
        downIdx = rotate(downIdx);

        if(robots[downIdx]) {
            robots[downIdx] = false;
        }
    }

    static void stepTwo() {
        int boundary = rotate(upIdx);
        for (int i = rotate(downIdx); i != boundary; i = rotate(i)) {
            int nextIdx = i + 1;
            if(nextIdx == N * 2) {
                nextIdx = 0;
            }
            if(robots[i] && !robots[nextIdx] && A[nextIdx] > 0) {
                robots[i] = false;
                setRobot(nextIdx);
            }
        }

        if (robots[downIdx]) {
            robots[downIdx] = false;
        }
    }
    
    static void stepThree() {
        if(A[upIdx] > 0) {
            setRobot(upIdx);
        }
    }

    static int rotate(int pos) {
        pos--;

        if(pos < 0) {
            return N * 2 - 1;
        }

        return pos;
    }
    
    static void setRobot(int idx) {
        robots[idx] = true;
        A[idx]--;
        if(A[idx] == 0) {
            zeroDurability++;
        }
    }
}