BOJ 2146 다리 만들기

https://www.acmicpc.net/problem/2146

문제

여러 섬으로 이루어진 나라가 있다. 이 나라의 대통령은 섬을 잇는 다리를 만들겠다는 공약으로 인기몰이를 해 당선될 수 있었다. 하지만 막상 대통령에 취임하자, 다리를 놓는다는 것이 아깝다는 생각을 하게 되었다. 그래서 그는, 생색내는 식으로 한 섬과 다른 섬을 잇는 다리 하나만을 만들기로 하였고, 그 또한 다리를 가장 짧게 하여 돈을 아끼려 하였다.

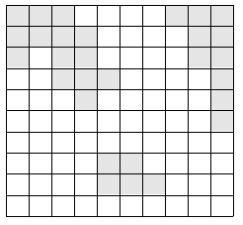
이 나라는 N×N크기의 이차원 평면상에 존재한다. 이 나라는 여러 섬으로 이루어져 있으며, 섬이란 동서남북으로 육지가 붙어있는 덩어리를 말한다. 다음은 세 개의 섬으로 이루어진 나라의 지도이다.

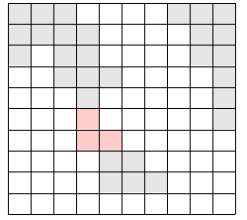
위의 그림에서 색이 있는 부분이 육지이고, 색이 없는 부분이 바다이다. 이 바다에 가장 짧은 다리를 놓아 두 대륙을 연결하고자 한다. 가장 짧은 다리란, 다리가 격자에서 차지하는 칸의 수가 가장 작은 다리를 말한다. 다음 그림에서 두 대륙을 연결하는 다리를 볼 수 있다.

물론 위의 방법 외에도 다리를 놓는 방법이 여러 가지 있으나, 위의 경우가 놓는 다리의 길이가 3으로 가장 짧다(물론 길이가 3인 다른 다리를 놓을 수 있는 방법도 몇 가지 있다).

지도가 주어질 때, 가장 짧은 다리 하나를 놓아 두 대륙을 연결하는 방법을 찾으시오.

---

입력

첫 줄에는 지도의 크기 N(100이하의 자연수)가 주어진다. 그 다음 N줄에는 N개의 숫자가 빈칸을 사이에 두고 주어지며, 0은 바다, 1은 육지를 나타낸다. 항상 두 개 이상의 섬이 있는 데이터만 입력으로 주어진다.

---

출력

첫째 줄에 가장 짧은 다리의 길이를 출력한다.

---

예제 입력 1

10
1 1 1 0 0 0 0 1 1 1
1 1 1 1 0 0 0 0 1 1
1 0 1 1 0 0 0 0 1 1
0 0 1 1 1 0 0 0 0 1
0 0 0 1 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 1 0 0 0 0
0 0 0 0 1 1 1 0 0 0
0 0 0 0 0 0 0 0 0 0

예제 출력 1

3

---

코드

오랜만에 푼 약간 난이도 있는 BFS 문제였던 것 같다.

문제를 푼 아이디어는 다음과 같다.

1. 각 섬에 해당하는 육지를 넘버링한다. ex) 2번 섬에 해당하는 모든 땅에 2 할당
2. 각 섬의 외곽에서 다른 육지까지의 최소 거리를 BFS로 계산한다.
3. 2번에서 계산한 거리 중 최소 거리를 정답으로 출력한다.

각 섬을 넘버링할 때는 DFS를 사용했다.

조금 유의해서 봐야할 부분은 2번이다.

섬의 외곽이란, 특정 육지에서 상하좌우에 있는 육지가 모두 같은 섬의 육지가 아닌 곳을 말한다.

즉, 특정 육지에서 BFS로 탐색할 때 같은 섬이 아닌 곳만 탐색하도록 조건을 추가하면 된다는 것이다. 이렇게 되면 자연스럽게 내륙(4면이 모두 같은 섬의 육지로 둘러쌓인 곳)은 탐색을 생략하게 된다.

import java.awt.*;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.Queue;
import java.util.StringTokenizer;

public class Main {

    static final int[] DIR_R = {1, -1, 0, 0};
    static final int[] DIR_C = {0, 0, 1, -1};
    static int N;
    static int[][] map;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        map = new int[N][N];
        for (int i = 0; i < N; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            for (int j = 0; j < N; j++) {
                map[i][j] = -Integer.parseInt(st.nextToken());
            }
        }

        // 각 섬에 해당하는 육지에 번호를 매긴다.
        numberingIslands();

        // 각 위치에서 가장 가까운 섬의 거리를 계산해서 그 중 가장 짧은 거리를 정답으로 출력
        int answer = Integer.MAX_VALUE;
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                if(map[i][j] != 0) {
                    int shortestDistance = findShortestDistance(i, j);
                    if(shortestDistance != -1) {
                        answer = Integer.min(answer, shortestDistance);
                    }
                }
            }
        }
        System.out.println(answer);
    }

    static void numberingIslands() {
        int numbering = 1;
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                if(map[i][j] == -1) {
                    dfs(i, j, numbering);
                    numbering++;
                }
            }
        }
    }

    static void dfs(int r, int c, int number) {
        map[r][c] = number;

        for (int i = 0; i < DIR_R.length; i++) {
            int newR = r + DIR_R[i];
            int newC = c + DIR_C[i];
            boolean isInside = newR >= 0 && newR < N && newC >= 0 && newC < N;
            if (isInside && map[newR][newC] == -1) {
                dfs(newR, newC, number);
            }
        }
    }

    /**
     * bfs로 가장 가까운 섬의 거리를 계산
     * @return 섬의 내륙 부분에 위치한 육지의 경우 -1, 그 외에는 가장 가까운 섬의 거리
     */
    static int findShortestDistance(int r, int c) {
        boolean[][] visited = new boolean[N][N];
        Queue<Point> queue = new ArrayDeque<>();
        queue.offer(new Point(r, c));
        visited[r][c] = true;
        int distance = 0;
        int number = map[r][c];
        for (; !queue.isEmpty(); distance++) {
            int size = queue.size();
            
            for (int i = 0; i < size; i++) {
                Point check = queue.poll();
                
                for (int j = 0; j < DIR_R.length; j++) {
                    int newR = check.x + DIR_R[j];
                    int newC = check.y + DIR_C[j];
                    boolean isInside = newR >= 0 && newR < N && newC >= 0 && newC < N;
                    
                    // 이동할 곳이 지도 안이고, 아직 방문하지 않았으며, 출발 섬의 육지가 아닐 경우, 검사 진행
                    if(isInside && !visited[newR][newC] && map[newR][newC] != number) {
                        // 이동할 곳이 출발 섬이 아닌 다른 섬일 경우, 거리 반환
                        if(map[newR][newC] != 0) {
                            return distance;
                        }

                        queue.offer(new Point(newR, newC));
                        visited[newR][newC] = true;
                    }
                }
            }
        }

        return -1;
    }
}